Algorithm Analysis (Big O) with Python
I started blogging about things that I care about to keep knowledge in my head and have these concepts present. I am not an expert on them, but the idea behind my posting about them is that at least I need to understand them and memorize some stuff.
Big O notation
Big O notation is one of the most fundamental tools for computer scientists to analyze the cost of an algorithm. It is a good practice for software engineers to understand in-depth as well.
Big-O notation signifies the relationship between the input and the steps required to execute the algorithm. It is denoted by a big “O” followed by an opening and closing parenthesis. Inside the parenthesis, the relationship between the input and the steps taken by the algorithm is presented using “n”. In plain words, Big O notation describes the complexity of your code using algebraic terms.
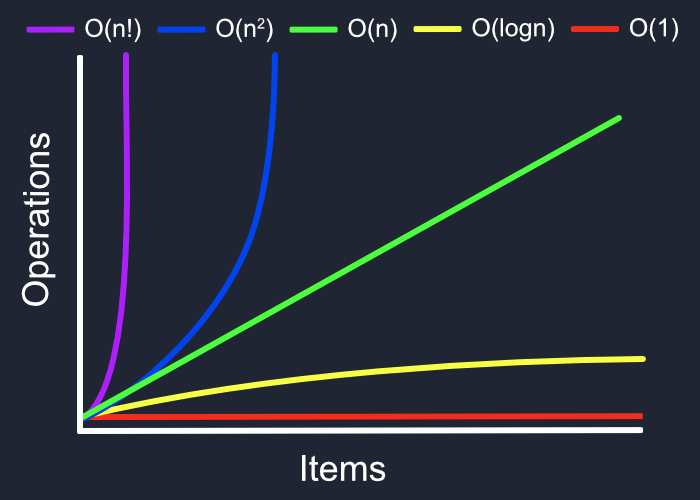
The following are some of the most common Big-O functions:
| Name | Big O |
|---|---|
| Constant | O(c) |
| Linear | O(n) |
| Quadratic | O(n^2) |
| Cubic | O(n^3) |
| Exponential | O(2^n) |
| Logarithmic | O(log(n)) |
| Log Linear | O(nlog(n)) |
Constant Complexity (O(C))
This is the ideal. No matter how many items there are, whether one or one million, the amount of time to complete will remain the same. Most operations that perform a single operation are O(1). Pushing to an array, getting an item at a particular index, adding a child element, etc., will all take the same amount of time regardless of the array length.
1
2
3
4
5
def constant_algo(items):
result = items[0] * items[0]
print(result)
constant_algo([4, 5, 6, 8])
In the above script, irrespective of the input size or the number of items in the input list, the algorithm performs only two steps: Finding the first element’s square and printing the result on the screen. Hence, the complexity remains constant.

Linear Complexity (O(n))
By default, all loops are an example of linear growth because there is a one-to-one relationship between the data size and time to completion. So an array with 1,000 times more items will take exactly 1,000 times longer.
1
2
3
4
5
def linear_algo(items):
for item in items:
print(item)
linear_algo([4, 5, 6, 8])
The complexity of the linear_algo function is linear in the above example since the number of iterations of the for-loop will equal the size of the input items array. For instance, if there are four items in the items list, the for-loop will be executed four times, and so on.

Quadratic Complexity (O(n^2))
Exponential growth is a trap we’ve all fall into at least once. Need to find a matching pair for each item in an array? Putting a loop inside a loop is an excellent way of turning an array of 1,000 items into a million operation search. It’s always better to have to do 2,000 operations over two separate loops than a million with two nested loops.
1
2
3
4
5
6
def quadratic_algo(items):
for item in items:
for item2 in items:
print(f"{item} {item2}")
quadratic_algo([4, 5, 6, 8])

Conclusion
The Big-O notation is the standard metric used to measure the complexity of an algorithm. Keeping your code as performant as possible may seem like an obvious concern, but I’m sure almost every developer has created double or triple nested loops at least once because ‘it just works’. Big O notation is essential in expressing and thinking about complexity.
Enjoyed this article? Support my work!
If you found this content helpful, consider buying me a coffee to show your appreciation.
Buy me a coffee